Week 11: Application: Navigation Using Fiducial Markers and Inertial Sensors
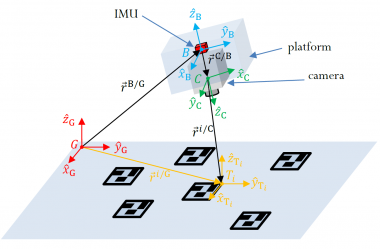
This week, I formule an aerospace/robotic application for the continuous-discrete filters. It consists of the navigation of a 6DOF platform equipped with inertial sensors (accelerometers and rate-gyros) as well as a camera. The scenario contains many fiducial markers placed at known positions. The visual fiducial system is assumed to be available; it provides indirect measures of the visible markers’ relative position w.r.t. the camera. In this application, we have to estimate the platform position, velocity, attitude, as well as the accelerometer and rate-gyro biases. Material: Continue→